import sys
def input():
return sys.stdin.readline().rstrip()
def check_pick(pick_list,point):
x,y = point
for nx,ny in pick_list:
if abs(nx-x) == abs(ny-y):
return False
return True
def dfs(problem_list,start,pick_list,color):
global result
if len(problem_list) == start:
result[color] = max(result[color],len(pick_list))
return
else:
for idx in range(start,len(problem_list)):
x,y = problem_list[idx]
if check_pick(pick_list,(x,y)):
dfs(problem_list,idx+1,pick_list+[(x,y)],color)
N = int(input())
arr = [list(map(int,input().split())) for _ in range(N)]
result = 0
black_set = []
white_set = []
for x in range(N):
for y in range(N):
if arr[x][y]:
if (x+y)%2:
white_set.append((x,y))
else:
black_set.append((x,y))
result = [0,0]
dfs(black_set,0,[],0)
dfs(white_set,0,[],1)
print(sum(result))문제를 푼 아이디어는 다음과 같다. 체스판은 흰색판과 검은색판으로 나뉘어져있다. 그리고 비숍이 잡아 먹을수 있는 위치는 같은 색깔에 있는 위치의 비숍일 뿐이다. 그러므로, 흰색과 검은색으로, 좌표를 나눠서, 각각 놓을 수 있는 최대 위치를 찾아주면 된다.
# chw0501님 코드 복기
import sys
def input():
return sys.stdin.readline()
def dfs(left_slash_num):
if visited[left_slash_num]:
return 0
visited[left_slash_num] = True
for right_slash_num in slash_dict[left_slash_num]:
if right_slash[right_slash_num] == -1 or dfs(right_slash[right_slash_num]):
left_slash[left_slash_num] = right_slash_num
right_slash[right_slash_num] = left_slash_num
return 1
return 0
N = int(input())
arr = [list(map(int,input().split())) for _ in range(N)]
right_slash = [-1 for _ in range(2*N+1)]
left_slash = [-1 for _ in range(2*N+1)]
slash_dict = [[] for _ in range(2*N+1)]
for x in range(N):
for y in range(N):
if arr[x][y]:
slash_dict[x+y].append(x-y+N)
result = 0
for left_slash_num in range(2*N):
visited = [False for _ in range(2*N)]
if dfs(left_slash_num):
result += 1
print(result)
더 빨리 풀 수 있는 코드는 대각선으로 나눠서 하는 방법인데 거기서 깔끔한 코드였던 chw0501님의 코드를 복기한 코드이다.
이 문제를 푸는방법은 다음과 같다. 한 위치에 비숍이 위치하면, 이 비숍의 X자 대각선으로는 다른 비숍들을 둘수 없다.
그렇다면, 흰색, 검은색으로만 나누지 말고, 대각선 위치를 기준으로 나눠 보는건 어떨까 라는 아이디어에서 출발된 것이다.
대각선을 (2*N-1)개씩 두 종류로 나뉠수 있다.

먼저 right_slash라고 부를, 오른쪽 아래로 향하는 대각선 모양은 다음과 같이 총 2*N-1개가 있다.
그러면 같은 대각선에 있는지 확인하는 방법은 행을 X 열을 Y로 했을때 (X-Y+N)으로 표현할 수 있다.
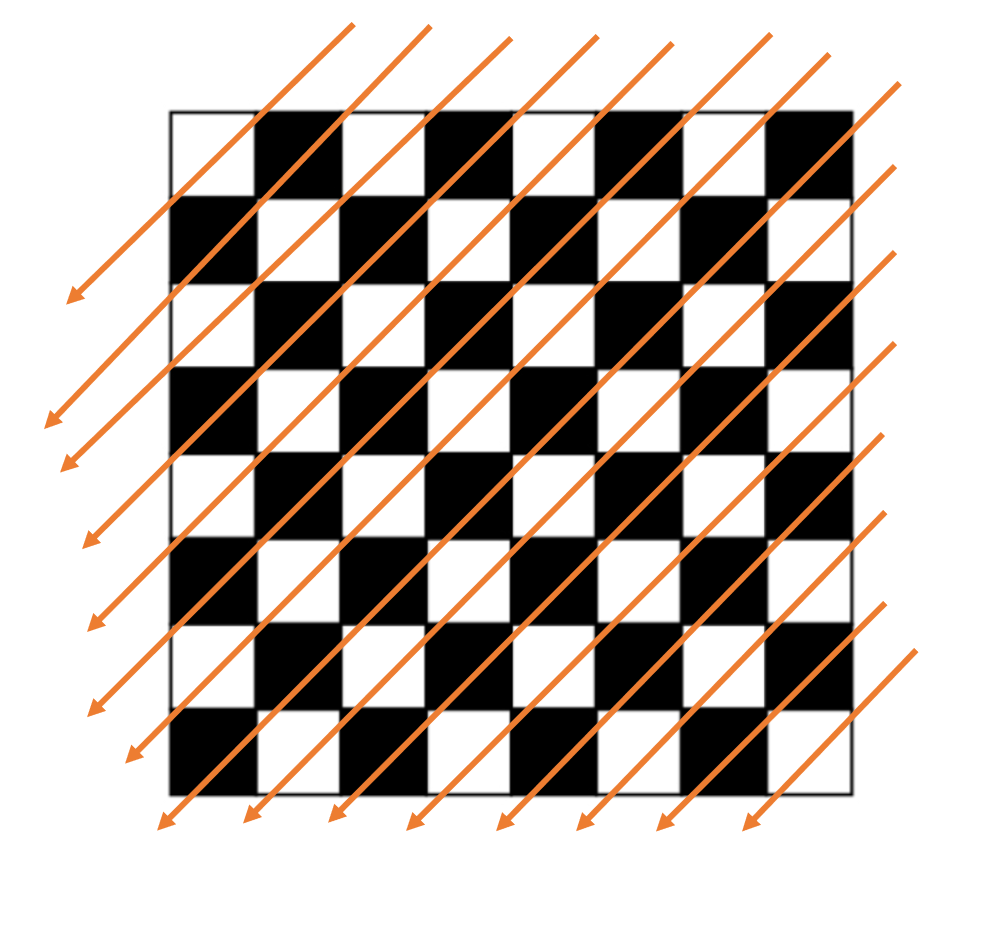
그리고 이렇게 좌측 아래로 향하는 슬래쉬를 left_slash라고 하겠다 이것도 위와 동일하게 2*N-1개가 생성되면
같은 집단인지 판별하는 방법은 (X+Y)이다.
그러면 우리는 해당 칸이 놓을수 있는 자리이면, left_slash를 구하고, 그 left_slash내에 해당 좌표의 right_slash 정보를 같이 집어넣어준다.
즉 slash_dict의 key 값은 left_slash의 좌표값이 되고, right_slash가 value가 되도록 넣어주면 된다.
이렇게 사전작업을 해놓은 상태에서 우리는 2개의 slash_list를 만들어놓는다.
각각 left_slash 와 right_slash로
해당의 index는 slash의 몇번째 위치에 있는지를 나타내며, 그 안의 value 값은 서로 반대편의 슬래쉬의 위치를 표시를 해주는 용도이다.
즉 left_slash의 3번째 위치에 5라는 값이 있으면,
3번째 left_slash에 있는 어떠한 점 중 하나를 골랐고, 그 점은 right_slash를 5를가지고 있다.를 의미한다.
즉 특정한 점을 만들 수 있는 것이다.
그러면 우리는 left_slah의 좌측아래로 향하는 슬래쉬를 기준으로 dfs를 진행을 해주면 된다.
def dfs(left_slash_num):
if visited[left_slash_num]:
return 0
visited[left_slash_num] = True
for right_slash_num in slash_dict[left_slash_num]:
if right_slash[right_slash_num] == -1 or dfs(right_slash[right_slash_num]):
left_slash[left_slash_num] = right_slash_num
right_slash[right_slash_num] = left_slash_num
return 1
return 0
이 dfs가 중요한데 이 dfs에서는 기본적으로 다음과 같다.
우리가 입력받은 left_slash_num에 저장된 right_slash_num들을 하나씩 가져온다.
right_slash라는 list에서 초기값으로 있으면 그 자리에 비숍을 놓을 수 있는 것이니,
left_slash에는 right_slash_num을 저장해주고, right_slash에는 left_slash_num을 저장을 해준다.
그러나 만약 해당 right_slash에 특정한 left_slash_num이 저장이 되어있다면,
우리는 위치를 조정해서 다시 놓을 수 있는지 확인을 해주는 것이다.
우리가 A_right라는 right_slash를 찾아볼려고 했더니 right_slash[A_right]의 값이 -1이 아니였고, B_left라는 값이 있었으면,
우리는 DFS를 통해 B_left를 다시 들어가서 B_left안에 있는 다른 right_slash들을 검사를 해서 놓을 수 있는지 확인을 해주는 것이다.
B_left 안에 [A_right,B_right,C_right] 등이 있다고하면,
이 중에 아직 right_slash가 -1인 값이 있으면, 우리는 그 위치를 조정해서 다시 비숍을 놓을 수 있을것이다.
그러나 이러한 경우가 하나도 없다면 비숍을 놓을 수 없기 때문에 0을 반환을 해주고,
한번 방문했던 곳을 다시 방문을 했다는 것은 사이클이 발생하고, 더 비숍을 놓을 곳이 없는것을 의미하기 때문에 0을 반환을 해주면된다.
위와 같은 dfs를 실행을 하면서 1을 반환이 되면, result의 값을 1씩 늘려주고,
최종적으로 result를 출력을 해주면 된다.
말로서 설명하기에는 어렵지만 디버깅도구를 통해 따라가보면 금방 이해할 수 있었다.
두번째 풀이는 이해하기 어려웠지만, 다른 사람의 코드를 보고 이런 방식으로도 할 수 있는걸 알았다.
좀 더 효율적인 방법이 있다는 걸 알고, 다음번에는 이런 코드를 짤 수 있도록 노력해야겠다.
'알고리즘 > 백준' 카테고리의 다른 글
| [BOJ/백준] 2213 트리의 독립집합 (0) | 2021.06.22 |
|---|---|
| [BOJ/백준] 1414 불우이웃 돕기 (0) | 2021.06.22 |
| [BOJ/백준] 2233 사과 나무 (0) | 2021.06.14 |
| [BOJ/백준] 1050 물약 (0) | 2021.06.14 |
| [BOJ/백준] 15653 구슬 탈출 4 (0) | 2021.06.14 |